Introduction
The cell environment
Cells are crowded and inhomogeneous. Its components are constantly undergoing transitions between different states via biochemical reactions. They are translocated actively or via diffusion while their movement is restricted by the shape of cell compartments. Biomolecules move either in 3d within the cell on a 2d surface within cell membranes. New proteins are constantly synthesized while others are broken down. Interactions between molecules drive phase separation and protein aggregation. This list of processes governing cells could go on. Depending on the research question at hand, we would like to be able to account for any of these features in a model.
As an example, synaptic plasticity at excitatory synapses is mediated mainly by a change in AMPA receptor number at the postsynaptic density (PSD) (Fig. 11). Of the different forms of synaptic plasticity that have been discovered, long-term potentiation (LTP) is the most noted (Fig. 12). Therefore, it is of great interest to understand how AMPARs are trafficked. However, this question is not easily answered as AMPARs have a multitude of interaction partners which are important for AMPAR targeting.
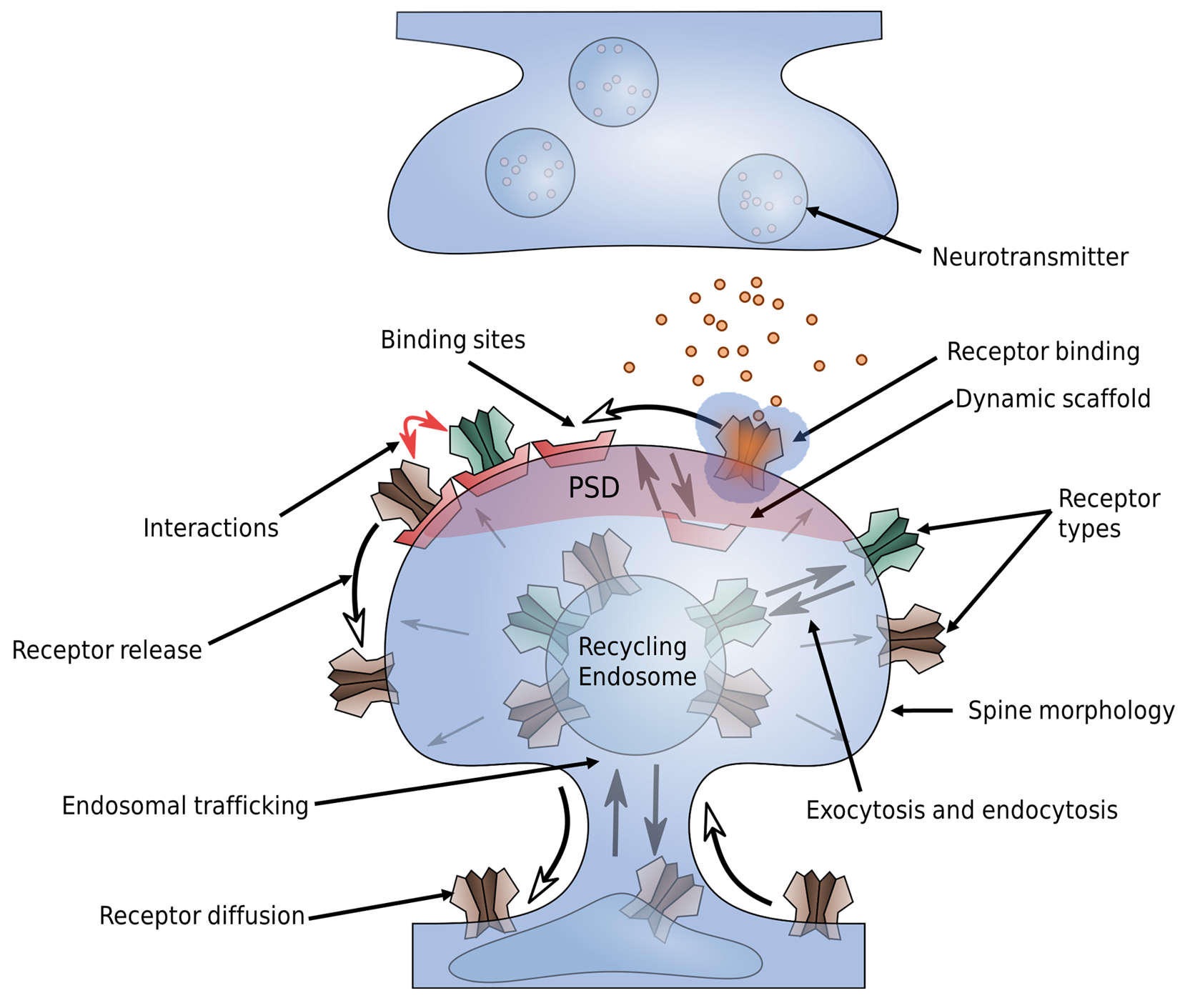
Fig. 11 AMPAR trafficking at the synapse. Whereas LTP, LTD but also homeostatic synaptic plasticity involve many different biomolecular processes, many of them target at some point the AMPA receptor, which mediates synaptic transmission at excitatory synapses. The trafficking of AMPARs can be related to various processes such as spine growth and receptor binding that are depicted in this figure.
The transmembrane domain of AMPARs forms a complex with various auxiliary proteins such as Stargazin. These auxiliary proteins interact with scaffolding proteins in the intracellular space of the postsynapse such as PSD95. In addition, trans-synaptic complexes composed, e.g., of neuroligin and neurexin bind to PS95 and presynaptic proteins such as N-cadherin are known to interact with AMPARs [36, 37]. The many proteins at synapses result in a crowded environment. In addition, the synaptic cleft only measures 20-30 nm in width. As such, effects of molecular crowding are accompanied by geometric restrictions.
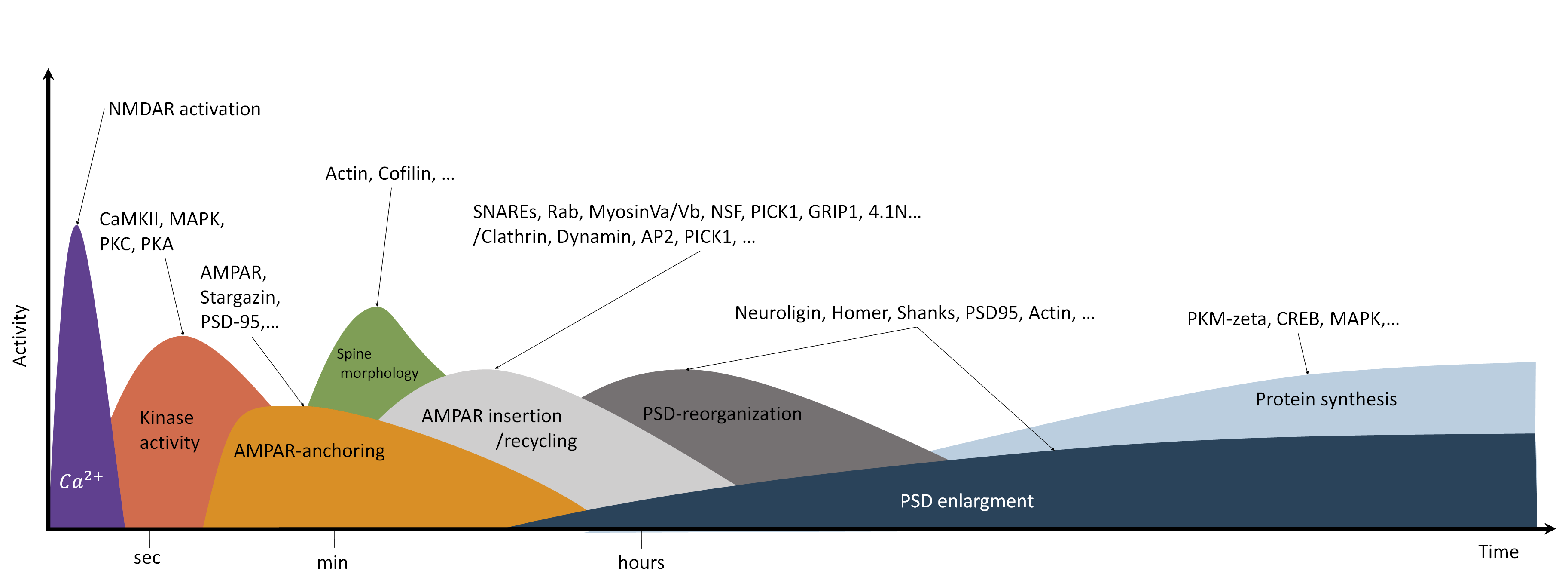
Fig. 12 Processes involved in synaptic plasticity (long-term potentiation). Long-term potentiation involves several different processes on different time- and spatial scales. High frequency stimulation and strong postsynaptic depolarization result in the influx of \(Ca^{2+}\). Calcium elevation occurs on the ms timescale and occurs locally in the dendrite and at dendritic spines [38]. Subsequently, calcium ions activate different kinases such as CaMKII, PKC and PKA. CaMKII in particular is essential for LTP induction. The activation of CaMKII is transient and occurs locally at the dendritic spine [39, 40]. The increased kinase activity triggers many subsequent processes. For example, phosphorylation of AMPAR subunits, PSD scaffolding proteins and auxiliary proteins such as Stargazin cause binding of additional AMPARs at the postsynaptic density [41, 42, 43, 44]. In addition, induction of LTP triggers spine growth, which also depends, among others, on CaMKII activation, F-actin elevation and cofilin [45, 46, 47]. LTP and spine growth are accompanied by enhanced protein recycling, endocytosis and exocytosis [48, 49, 50]. Maintenance and expression of late LTP depends on the synthesis of new proteins [51, 52]. Protein synthesis, actin dynamics and translocation result in the reorganization and growth of the PSD [53, 54, 55, 56, 57].
As mentioned above, the trafficking of transmembrane proteins such as AMPARs that move on a 2d surface while inside the membrane is governed also by their interaction with intracellular scaffolding proteins that move in 3d space such as PSD95. In order to fully understand AMPAR trafficking we may also want to investigate the behaviour of the intracellular interaction partners. In a series of experiments, [58, 59, 60] have shown that the PSD proteins PSD95, Shank, SynGAP and Homer undergo liquid-liquid phase separation (LLPS) in vitro, raising the assumption that also in vivo the PSD may form via a similar mechanism. Indeed, many proteins have been found to form liquid like condensates and this topic has gained a lot of attention in recent years as LLPs has many properties that seem to be important for cell functions in that it enables compartmentalization in the presence of constant protein exchange [61]. Indeed, experimental studies have found that the PSD is not entirely rigid but able to change its structure and composition under control conditions and in response to synaptic plasticity [54, 57, 62]. This raises several questions, e.g, of how stable are PSD condensates, and under what conditions do they form? Also, how does the interaction with transmembrane proteins shape the composition, structure and stability of such condensates?
Importantly, erroneous factors that bias LLPS can lead to pathological conditions via protein aggregation. As such, LLPS might have implications for diseases such as Alzheimer, ALS, and cancer [63, 64, 65]. A better understanding of phase separation is therefore of great interest in general as well as a possible mechanism involved in synaptic transmission and plasticity. The geometric restrictions at the synaptic cleft are also of great importance for experimental procedures. Fluorescent labeling of proteins often involve antibodies that can be 10-20 nm in size, impairing AMPAR movement inside and in the vicinity of the synaptic cleft [66]. However, the effects of crowding and of large probes at the synaptic cleft have not been investigated apart from [66] such that older experimental results may need to be reevaluated. Computer models could help to better understand these effects and to better interpret experimental data.
To summarize, their exist several open questions of which here only very few have been addressed:
How is receptor trafficking influenced by different crowded environments, by the interaction with other molecules and by synapse geometry.
How do PSD composition and structure influence receptor distributions and vice versa.
Under what conditions do the PSD proteins undergo phase separation and how stable is the PSD? How is the phase behaviour of the PSD shaped by the interaction with transmembrane proteins?
…
If we want to understand synaptic transmission and plasticity in more detail, we should take into account the structure of the PSD, the spine morphology and multivalent protein-protein interactions and we need to ask how these factor might influence receptor distribution and trafficking. This becomes important especially in the light of diseases. Synaptic signaling, neuronal growth etc. are robust also because their exists some redundancy in protein function. However, sometimes a small bias can result in erroneous functioning. To understand when and under what conditions these may arise we need to study not only the single proteins but we need to put these into an environment where they can interact in large populations. For this, however, we need powerful and especially flexible tools that can be relatively quickly adapted to target a new research question. In the following chapter I will introduce PyRID, a new tool for reaction diffusion simulations of interacting particles.
Modeling approaches
One big problem that arises not only in terms of modeling synaptic plasticity but for many cell processes in general are the different time and spatial scales at which these processes occur as well as the large number of complex molecules involved. A number of cell processes can be simulated on the required time scale by using simplifications. Various methods utilizing different approximations have therefore been developed (Fig. 13). For example, large signaling pathways can be formulated in terms of systems of ODEs, also termed reaction rate equations in this setting, or in terms of chemical master equations which can be solved efficiently using stochastic simulation algorithms such as the Gillespie SSA [67, 68]. However, this approach neglects most aspects of the cellular environment, e.g. by assuming a well mixed, homogeneous system. Also, intrinsic time delays are not captured out of the box but can be accounted for to some degree by a multi-compartment description where molecules hop between compartments. Therefore, it is often required to add spatial dimensions. This can be done, using voxel- (3D) or lattice- (2D) based methods, i.e. we solve our chemical master equation per voxel and simulate diffusion by means of molecules hopping between voxels. However, the approach does assume that within each voxel the system is well mixed and that the voxel size is much larger than the size of the molecules. Therefore, The voxel based approach is mainly useful for large scale simulations but breaks down for smaller systems. System scales above \(\mu m\) and on time scales of minutes are feasible. In this regard, the synapse and sub-synaptic structures such as the PSD have to be considered as small systems. Similarly, the ODE approach can be extended to partial differential equations to include spatial dimensions. However, the PDE approach underlies similar limitations and is not well suited for small scale simulations with just a few hundred molecules. For models of the synapse and sub-synaptic structures, particle based approaches are therefore much better suited. A review on the above discussed approaches can also be found in [68]. There exist many particle-based simulation methods. All atom molecular dynamics simulations model the system of interest in great detail, however are not suitable to investigate processes on larger scales, i.e., consisting of hundreds to thousands of proteins and that take place on a micrometer scale (size of the synapse). As such, coarse-graining approaches are necessary where groups of atoms are approximated by single beads. The level of coarse-graining can range from single amino acids to arbitrary reductions of the polypeptide chain of the proteins [69, 70]. Mesoscopic molecular dynamics takes this approach to the extreme and allows for the simulation of thousands of proteins. Instead of representing proteins per atom or per amino sequence, each protein is reduced to a minimal representation of its excluded volume, i.e. an approximation of its average rigid shape, and the interaction sites that are of interest in a specific scenario, which may be represented by a single particle. Thereby, in the minimal case, molecules are represented as patchy particles [30]. Tools by which either of the above approaches can be implemented are, e.g. LAMMPS, Gromacs or HooMD. Coarse graining is a large field of research itself and many problems such as defining a proper force field have to be solved. However, a discussion on this topic is way beyond the scope of this work. A review on coarse grained protein models can be found ,e.g., in [69]. Whereas mesoscopic molecular dynamics allows for the simulation of the interaction of hundreds of proteins, reaction kinetics are, however, usually neglected. The particle based reaction diffusion approach simulates the Brownian dynamics of molecules and also includes stochastic simulation algorithms for uni- and biomolecular reactions [10, 71]. However, most particle-based reaction diffusion models represent molecules as points and neglect force fields and pairwise particle interactions. Therefore, whereas this simplification allow for even larger simulations than the mesoscopic MD approach with 10 thousands of molecules and time scales on the order of \(\mu s-s\), it is often unrealistic, especially in crowded environments. Popular tools for particle-based reaction diffusion simulations are, e.g., MCell (CellBlender) and Smoldyn. The only particle-based reaction diffusion simulator that accounts for particle interactions via potential energy functions is ReaDDy. However, ReaDDy does out of the box not support simulations in arbitrary 3D geometries and is also not well suited for mesoscopic modeling as defined above as it does not support rigid bead models of molecules. Therefore, I here introduce a new tool named PyRID, which is a Python based simulator for reaction-diffusion models of interacting particles. PyRID runs about as fast as ReaDDy, is flexible and modifiable and supports 3D mesh geometries, surface diffusion, rigid bead models and many types of uni and bimolecular reactions. A comparison of features between PyRID, ReaDDy, MCell and Smoldyn is shown in Fig. 14.
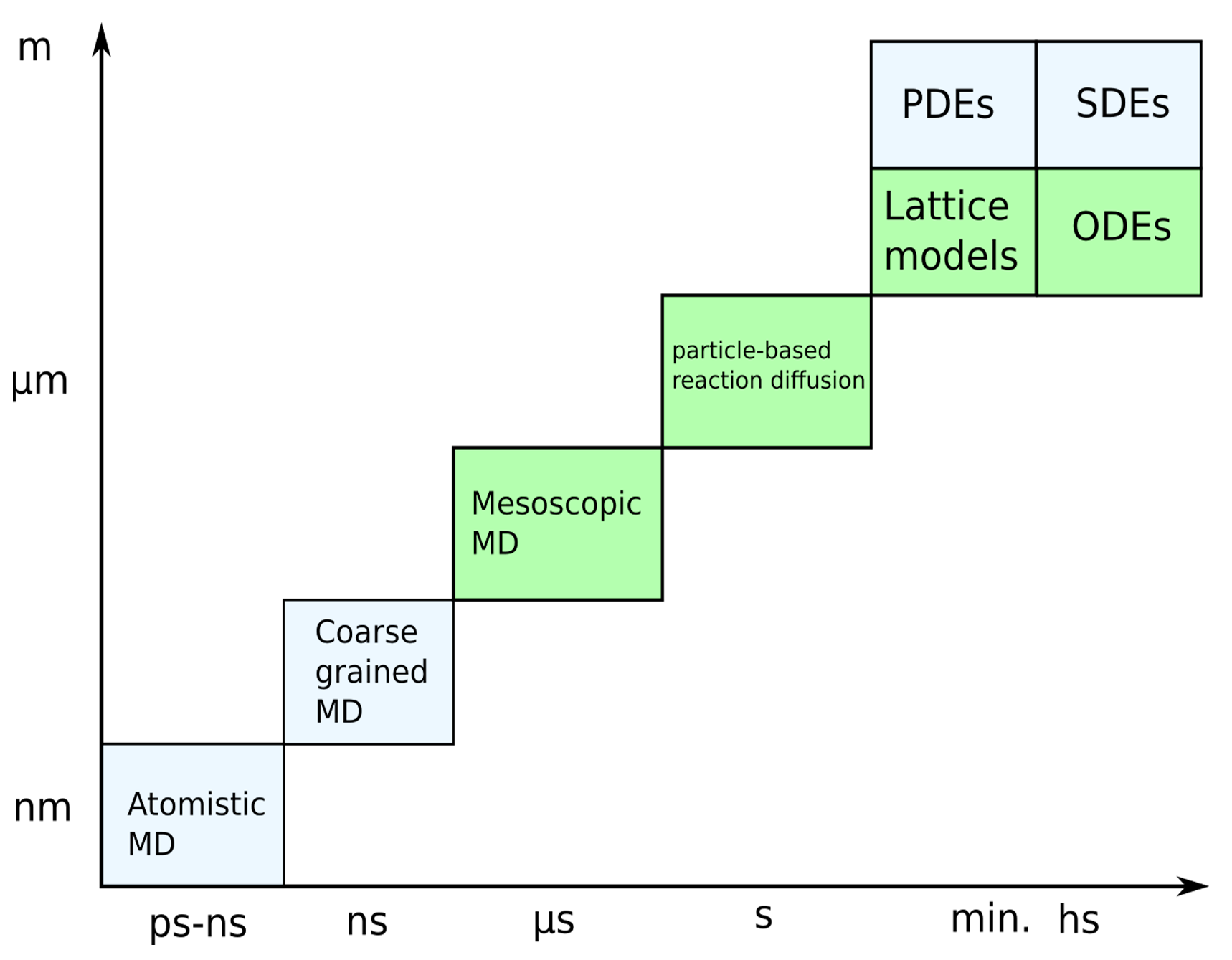
Fig. 13 Modeling approaches. Independent of whether one models the individual signaling pathways or processes such as exocytosis and spine growth, the question of the method is important. As discussed in the text, all-atom molecular dynamics are in principle capable of replicating all the processes we are interested in but are by far too computationally expensive. Such, only simulations on the nm spatial and the ns time-scale are possible. Therefore, coarse graining and mean field approaches are necessary. These, however, come at the cost of of neglecting many details. At the extreme, ordinary differential equations neglect any spatial and stochastic properties and are therefore suited to model processes on very long time scales. Intermediate approaches such as particle based reaction diffusion simulations or mesoscopic molecular dynamics are able to simulate biochemical reactions and molecular interactions by rate based approaches and coarse grained force fields. Which method to use strongly depends on the scientific question.

Fig. 14 Feature comparison. Please note that this feature comparison is not complete and biased towards PyRID as only the main features of PyRID are compared to the other tools. Each of the tools mentioned here have some unique abilities and features that are not necessarily supported by the other tools or PyRID. However, to do an all-encompassing comparison would go beyond the scope of this work.